Floyd判圈算法(Floyd Cycle Detection Algorithm) 又称为“龟兔赛跑算法”，是一个可以在有限状态机/链表/迭代函数上判断是否有环并求出环的长度和起点的算法。

基本思想

以后使用链表举例，状态机和迭代函数基本同理。
在连表上放置一个快指针和一个慢指针，快指针每次沿链表前进两格（或更多），慢指针则前进一格；如果链表上存在环，快指针就会先于慢指针进入环并在其中循环，等到慢指针进入环之后，快慢指针终会相遇（即快指针扣圈慢指针）。

求解环长与起点

环长比较简单，两指针相遇之后让一个指针原地不动，另一个沿着环再来一圈并计数即可得到环长，重点讨论如何查找环的起点。

查找起点

方法

设两指针相遇于B点，则两指针相遇之后使一个指针回到链表起点，另一个指针在B点；两指针同时一步一步向前移动，两者再次相遇的点就是环的起点。

原理

设两指针相遇时慢指针所走过的距离为i，走过的圈数为a；
链表头到链表起点的距离为m;
环的长度为n；
相遇位置B点与起点的距离为k；
则有：
i=m+an+k
则快指针有：
2i=m+bn+k
两式相减可得：
i=(a-b)n
即i是圈长n的整数倍

如此即可得到当头指针沿链表前进m步之后，另一个指针距离起点i+m，而i又是圈长的整数倍，所以两指针在环的起点处相遇。

例题

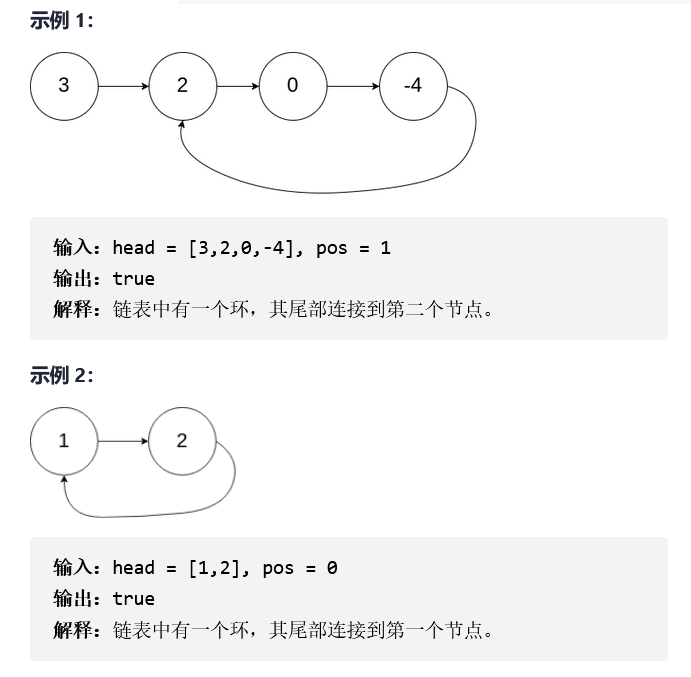
给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

如果链表中存在环，则返回 true 。 否则，返回 false 。

进阶：

你能用 O(1)（即，常量）内存解决此问题吗？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/linked-list-cycle
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

常规解法

哈希表，太LOW了此处省略

Floyd

public class Solution {
    public boolean hasCycle(ListNode head) {
        ListNode fast, slow;
        if(head == null)    return false;

        fast = head.next; slow = head;  //此处不让两指针一起出发是为了后面while的条件更好写
        //但是这种写法会使得求圈起点时需要将slow放回头结点后fast自己先走一格，原因可以从公式中推出
        while(fast != slow){
            try{
                fast = fast.next.next;
            }catch(Exception e){
                return false;
            }
            slow = slow.next;
        }
        return true;
    }
}